Cross-Validation: Techniques, Pitfalls, and Best Practices
Why Cross-Validation is the lie detector of your ML model...
What is Cross-Validation and Why it Matters
Cross-Validation (CV) is a method to test your model’s honesty.
A single train-test split can fool you. It might make a weak model look good by chance. CV fixes this by evaluating performance across multiple data splits, giving a more reliable estimate.
Overfitting? High train score and low CV score. Means high variance.
Underfitting? Both scores low. Means high bias.
Think of it as a stress test for your model - revealing how well it performs in different scenarios. And evaluating performance across CV folds, you can pick the best model or hyperparameters during model training.
After all, one split can lie. Cross-validation doesn’t.
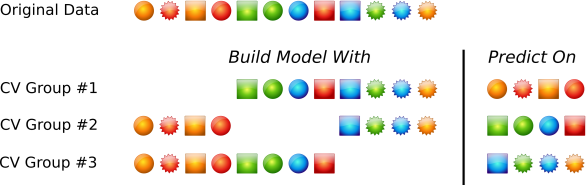
How Cross-Validation Works
Below is a pictorial representation of how CV works (Source: Max Kuhn, Applied Predictive Modeling):
Average the performance metrics across prediction folds. The result is an unbiased estimate of generalized error assuming no leakage.
And how does it work along with parameter selection in a grid search?
Illustration
Say you want to try three possible values of a hyper-parameter m = [20, 30, 40]. After a 3 fold CV, the below results are obtained:
Selected m = 30 with best cross-validated performance.
Where CV Helps and Where it Doesn’t
Why CV is Rare in Deep Learning
Training a deep neural network with millions of parameters K times is super expensive due to the high compute cost.
The common approach is to use a train/validation/test split with early stopping.
Also, it’s a good practice to keep a final unseen test set.
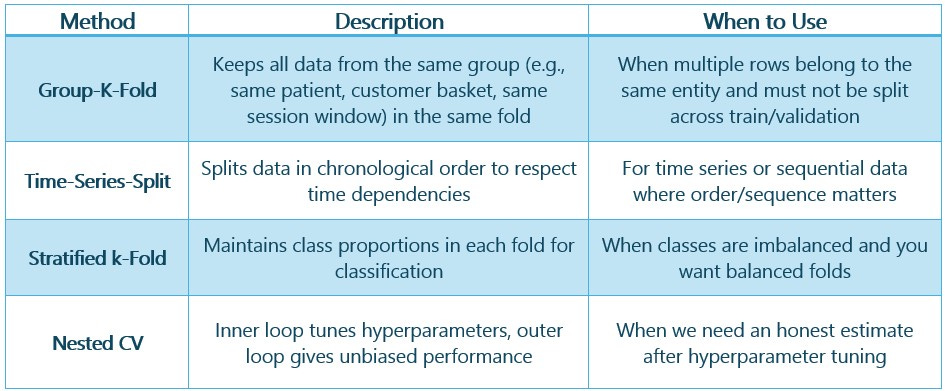
Common CV Methods
There are several types of CV methods as shown below:
A Few Important Things to Note
1. CV and Bias/Variance
Cross-validation (CV) doesn’t reduce bias or variance. It simply gives you a more unbiased estimate of total error (MSE).
Let’s break it down:
Bias: Error from overly simple assumptions (e.g., fitting a straight line to a curve).
Variance: Error from model instability i.e. small data changes lead to large prediction shifts.
The total expected error is:
Total Error (MSE) = Bias² + Variance + Irreducible Noise
Let’s see an example:
True value = 50
Model predictions on 3 resampled datasets = 42, 56, 50
Average prediction = 49.33
Bias² = (49.33 - 50)² = 0.44
Variance = mean squared deviation from the average = (1/n) × sum[(xᵢ − x̄)²]
Or, Variance = [(42 - 49.33)2 + (56 - 49.33)2 + (50 - 49.33)2] / 3 = 32.89
Total error = 33.33
CV with grid search evaluates several model parameters to identify the configuration with the lowest cross-validated error. So, CV is rather a model selection process and not an error minimization algorithm in itself.
Now, the standard k-fold CV won’t give us bias² and variance separately, since each point is predicted once. To estimate these components, we need multiple predictions per point, like repeated CV or bootstrapping.
2. Example of 3-Fold Nested CV:
Imagine the data is split into three parts: D1, D2, and D3.
Inner CV fold is used to tune while the outer CV folds give unbiased performance estimate, unlike the regular K-Fold CV.
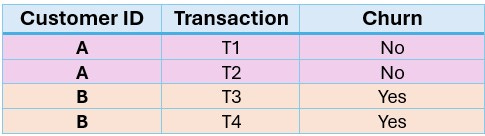
3. Where We Need Group-K-Fold
Imagine you're building a model to predict customer churn, and each customer has multiple transactions:
If you use regular k-Fold, T1 might go to training and T2 to validation and leaking customer behaviour. Group-K-Fold keeps all of customer A's data together, preserving independence between folds and avoiding data leakage during cross-validation.
Other similar examples are shopping sessions, patient records, sensor batch, and user ID-specific activities. In such cases, Group-K-Fold is used to keep multiple data points belonging to the same entity together.
4. Picking the Right CV Strategy
5. Common Pitfalls and the Fix
6. Why Decision Trees Have High Variance
Decision trees use greedy, local splits that are highly sensitive to small data changes. A minor variation like a new row or an outlier - can change the first split and ripple through the entire tree, leading to drastically different models.
Since they don’t globally optimize or backtrack, this recursive structure makes them unstable and prone to overfitting, especially with deep trees.
Using Random Forests or other ensemble methods helps address the variance problem.
By aggregating predictions from multiple trees trained on different data subsets, these models stabilize performance and reduce sensitivity to small data changes.
7. Some Best Practices & Takeaways
Cross-validation improves the model evaluation process but cannot guarantee generalization.
Always do pre-processing inside the CV loop - otherwise there may be data leakage.
Be leakage-aware: no scaling, encoding, or feature selection before CV.
For tuning, nested CV works better.
Use Stratified-K-Fold, Time-Series-Split, and Group-K-Fold where appropriate as mentioned above.
Reference
Kuhn, M., & Johnson, K. (2013). Applied Predictive Modeling. Springer.
Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer.
Chollet, F. (2021). Deep Learning with Python (2nd Edition). Manning.